hook在维基百科中定义:钩子编程(hooking),也称作“挂钩”,是计算机程序设计术语,指通过拦截软件模块间的函数调用、消息传递、事件传递来修改或扩展操作系统、应用程序或其他软件组件的行为的各种技术。处理被拦截的函数调用、事件、消息的代码,被称为钩子(hook)。
Hook 是 PyTorch 中一个十分有用的特性。利用它,我们可以不必改变网络输入输出的结构,方便地获取、改变网络中间层变量的值和梯度 。这个功能被广泛用于可视化神经网络中间层的 feature、gradient,从而诊断神经网络中可能出现的问题,分析网络有效性。本文将结合代码,由浅入深地介绍 pytorch 中 hook 的用法。本文分为三部分:
Hook for Tensors :针对 Tensor 的 hook
Hook for Modules:针对例如 nn.Conv2dnn.Linear等网络模块的 hook
Guided Backpropagation:利用 Hook 实现的一段神经网络可视化代码
Hook for Tensors 在pytorch docs搜索hook,可以发现有四个hook相关的函数,分别为register_hook,register_backward_hook,register_forward_hook,register_forward_pre_hook。其中register_hook属于tensor类,而后面三个属于moudule类。
在 PyTorch 的计算图(computation graph)中,只有叶子结点(leaf nodes)的变量会保留梯度。而所有中间变量的梯度只被用于反向传播,一旦完成反向传播,中间变量的梯度就将自动释放,从而节约内存。如下面这段代码所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 X---------- W ------ - - -----> + ---> Z ---> * ---> O - Y---------- import torch x = torch.Tensor([0, 1, 2, 3]).requires_grad_() y = torch.Tensor([4, 5, 6, 7]).requires_grad_() w = torch.Tensor([1, 2, 3, 4]).requires_grad_() z = x+y # z.retain_grad() o = w.matmul(z) o.backward() # o.retain_grad() print('x.requires_grad:', x.requires_grad) # True print('y.requires_grad:', y.requires_grad) # True print('z.requires_grad:', z.requires_grad) # True print('w.requires_grad:', w.requires_grad) # True print('o.requires_grad:', o.requires_grad) # True print('x.grad:', x.grad) # tensor([1., 2., 3., 4.]) print('y.grad:', y.grad) # tensor([1., 2., 3., 4.]) print('w.grad:', w.grad) # tensor([ 4., 6., 8., 10.]) print('z.grad:', z.grad) # None print('o.grad:', o.grad) # None
由于 z 和 o 为中间变量(并非直接指定数值的变量,而是由别的变量计算得到的变量),它们虽然 requires_grad 的参数都是 True,但是反向传播后,它们的梯度并没有保存下来,而是直接删除了,因此是 None。如果想在反向传播之后保留它们的梯度,则需要特殊指定:把上面代码中的z.retain_grad() 和 o.retain_grad的注释去掉,可以得到它们对应的梯度,运行结果如下所示:
1 2 3 4 5 6 7 8 9 10 x.requires_grad: True y.requires_grad: True z.requires_grad: True w.requires_grad: True o.requires_grad: True x.grad: tensor([1., 2., 3., 4.]) y.grad: tensor([1., 2., 3., 4.]) w.grad: tensor([ 4., 6., 8., 10.]) z.grad: tensor([1., 2., 3., 4.]) o.grad: tensor(1.)
但是,这种加 retain_grad() 的方案会增加内存占用,并不是个好办法,对此的一种替代方案,就是用 hook 保存中间变量的梯度。
对于中间变量z,hook 的使用方式为:z.register_hook(hook_fn),其中 hook_fn 为一个用户自定义的函数,其签名为:
1 hook_fn(grad) -> Tensor or None
它的输入为变量 z 的梯度,输出为一个 Tensor 或者是 None (None 一般用于直接打印梯度)。反向传播时,梯度传播到变量 z,再继续向前传播之前,将会传入 hook_fn。如果 hook_fn的返回值是 None,那么梯度将不改变,继续向前传播,如果 hook_fn的返回值是 Tensor 类型,则该 Tensor 将取代 z 原有的梯度,向前传播。
下面的示例代码中 hook_fn 不改变梯度值,仅仅是打印梯度:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import torch x = torch.Tensor([0, 1, 2, 3]).requires_grad_() y = torch.Tensor([4, 5, 6, 7]).requires_grad_() w = torch.Tensor([1, 2, 3, 4]).requires_grad_() z = x+y # =================== def hook_fn(grad): print(grad) z.register_hook(hook_fn) # =================== o = w.matmul(z) print('=====Start backprop=====') o.backward() print('=====End backprop=====') print('x.grad:', x.grad) print('y.grad:', y.grad) print('w.grad:', w.grad) print('z.grad:', z.grad)
运行结果如下:
1 2 3 4 5 6 7 =====Start backprop===== tensor([1., 2., 3., 4.]) =====End backprop===== x.grad: tensor([1., 2., 3., 4.]) y.grad: tensor([1., 2., 3., 4.]) w.grad: tensor([ 4., 6., 8., 10.]) z.grad: None
我们发现,z 绑定了hook_fn后,梯度反向传播时将会打印出 o 对 z 的偏导,和上文中 z.retain_grad()方法得到的 z 的偏导一致。
接下来可以试一下,在 hook_fn 中改变梯度值,看看会有什么结果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 import torch x = torch.Tensor([0, 1, 2, 3]).requires_grad_() y = torch.Tensor([4, 5, 6, 7]).requires_grad_() w = torch.Tensor([1, 2, 3, 4]).requires_grad_() z = x + y # =================== def hook_fn(grad): g = 2 * grad print(g) return g z.register_hook(hook_fn) # =================== o = w.matmul(z) print('=====Start backprop=====') o.backward() print('=====End backprop=====') print('x.grad:', x.grad) print('y.grad:', y.grad) print('w.grad:', w.grad) print('z.grad:', z.grad)
运行结果如下:
1 2 3 4 5 6 7 =====Start backprop===== tensor([2., 4., 6., 8.]) =====End backprop===== x.grad: tensor([2., 4., 6., 8.]) y.grad: tensor([2., 4., 6., 8.]) w.grad: tensor([ 4., 6., 8., 10.]) z.grad: None
发现 z 的梯度变为两倍后,受其影响,x和y的梯度也都变成了原来的两倍。在实际代码中,为了方便,也可以用 lambda 表达式来代替函数,简写为如下形式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import torch x = torch.Tensor([0, 1, 2, 3]).requires_grad_() y = torch.Tensor([4, 5, 6, 7]).requires_grad_() w = torch.Tensor([1, 2, 3, 4]).requires_grad_() z = x + y # =================== z.register_hook(lambda x: 2*x) z.register_hook(lambda x: print(x)) # =================== o = w.matmul(z) print('=====Start backprop=====') o.backward() print('=====End backprop=====') print('x.grad:', x.grad) print('y.grad:', y.grad) print('w.grad:', w.grad) print('z.grad:', z.grad)
运行结果和上面的代码相同,我们发现一个变量可以绑定多个 hook_fn,反向传播时,它们按绑定顺序依次执行。例如上面的代码中,第一个绑定的 hook_fn把 z的梯度乘以2,第二个绑定的 hook_fn打印z的梯度。因此反向传播时,也是按照这个顺序执行的,打印出来的 z的梯度值,是其原本梯度值的两倍。
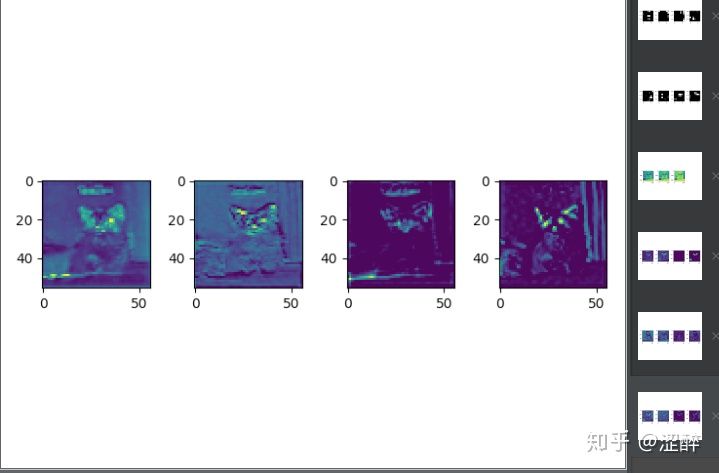
特征图打印应用:直接利用pytorch已有的resnet18进行特征图打印,只打印卷积层的特征图,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 import torch from torchvision.models import resnet18 import torch.nn as nn from torchvision import transforms import matplotlib.pyplot as plt def viz(module, input): x = input[0][0] #最多显示4张图 min_num = np.minimum(4, x.size()[0]) for i in range(min_num): plt.subplot(1, 4, i+1) plt.imshow(x[i].cpu()) plt.show() import cv2 import numpy as np def main(): t = transforms.Compose([transforms.ToPILImage(), transforms.Resize((224, 224)), transforms.ToTensor(), transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) ]) device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") model = resnet18(pretrained=True).to(device) for name, m in model.named_modules(): # if not isinstance(m, torch.nn.ModuleList) and \ # not isinstance(m, torch.nn.Sequential) and \ # type(m) in torch.nn.__dict__.values(): # 这里只对卷积层的feature map进行显示 if isinstance(m, torch.nn.Conv2d): m.register_forward_pre_hook(viz) img = cv2.imread('./cat.jpeg') img = t(img).unsqueeze(0).to(device) with torch.no_grad(): model(img) if __name__ == '__main__': main()
第一层卷积层输入
第四层卷积层的输入
模型大小,算力计算, 同样的用法,可以直接参考pytorch-summary 这个项目。
Hook for Modules 网络模块 module 不像上一节中的 Tensor,拥有显式的变量名可以直接访问,而是被封装在神经网络中间。我们通常只能获得网络整体的输入和输出,对于夹在网络中间的模块,我们不但很难得知它输入/输出的梯度,甚至连它输入输出的数值都无法获得。除非设计网络时,在 forward 函数的返回值中包含中间 module 的输出,或者用很麻烦的办法,把网络按照 module 的名称拆分再组合,让中间层提取的 feature 暴露出来。
为了解决这个麻烦,PyTorch 设计了两种 hook:register_forward_hook 和 register_backward_hook,分别用来获取正/反向传播时,中间层模块输入和输出的 feature/gradient,大大降低了获取模型内部信息流的难度。具体用法参考半小时学会 PyTorch Hook 。
参考:https://zhuanlan.zhihu.com/p/73868323 https://github.com/sksq96/pytorch-summary https://oldpan.me/archives/pytorch-autograd-hook https://pytorch.org/docs/stable/search.html?q=hook&check_keywords=yes&area=default