topk(input, k, dim=None, largest=True, sorted=True, out=None) -> (Tensor, LongTensor)
Semantics:
Returns the :attr:k largest elements of the given :attr:input tensor, a long a given dimension.

example:
1 | >>input = torch.tensor([[-3., -1., -2., -8., -7., -4., -9., -6.], |
Select topk value – Radix select
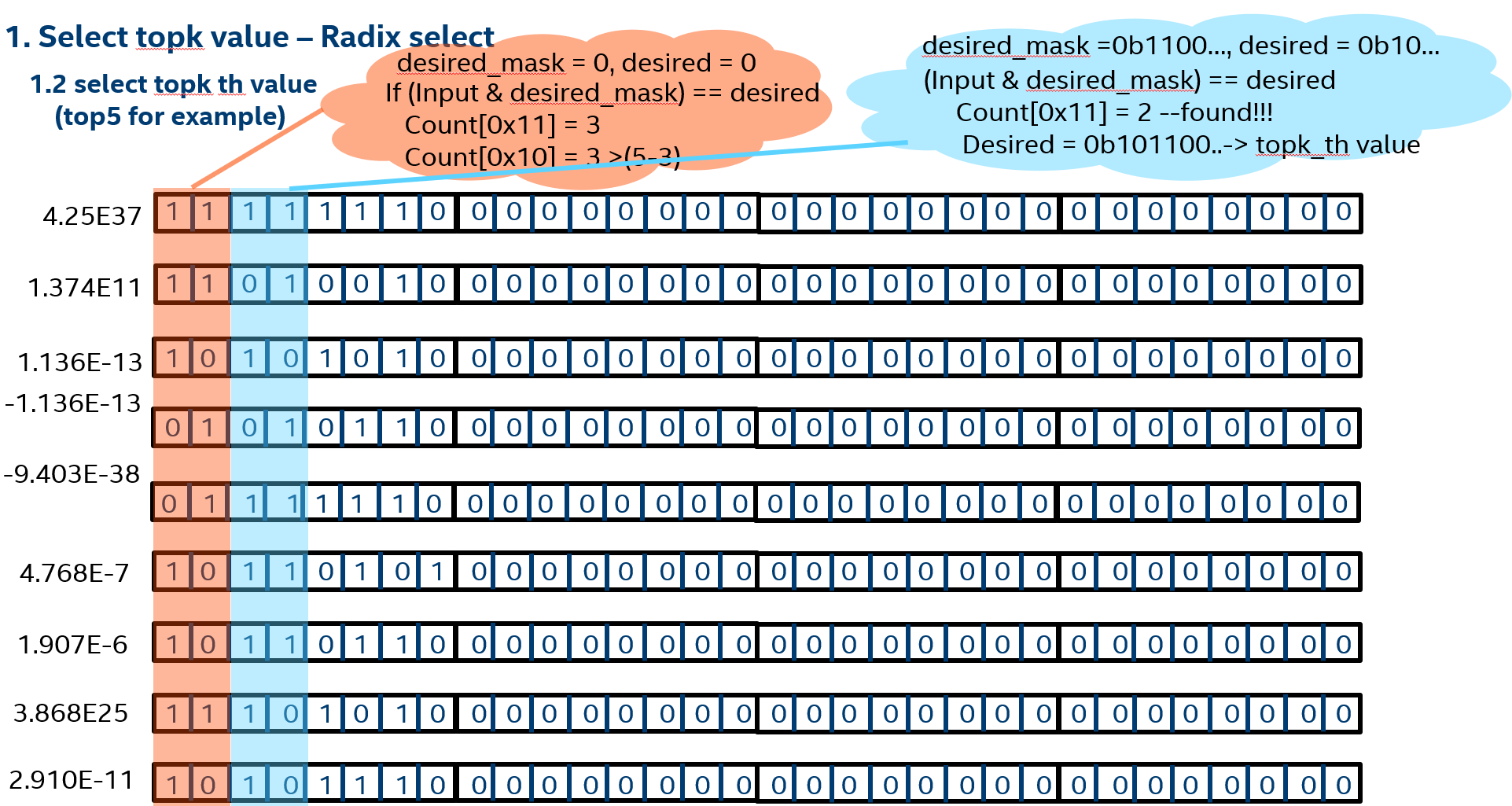
Radix select is not a comparison select but a counting select algorithm. When we select n bit keys, 2n counts are prepared for each number.
Simple Example:
1 | # Get top5 data |
Step0: count[0x11 & input] ++;
Step1: count[0x11] = 3, remain= 2
Step2: count[0x10] = 3, count > remain – found 5th topk value
Step3: has_topk = (input >= 5th topkvalue)
convert fp32 to uint32
Radix select assume all the data is unit32 type, so we need to convert float32 to unint32, double to uint64 first.

test file:
1 | #include <stdio.h> |
run:
1 | $ g++ -g float.c -o float |

Select topk value – Radix select
exclusive prefix scan
Now, we got topk th value: desired value got from previous step, but we don’t know at what index to write out the resulting values.
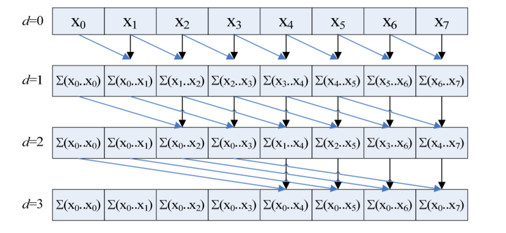
Inorder to get this, we performance an exclusive prefix sum of “hasTopk”, this will return the resulting index into which we need to write the result, if a thread has a result.
1 | bool hasTopK = (input_value >= topKValue); |
Store hasTopK into shared local memory: smem[thread_id] = hasTopK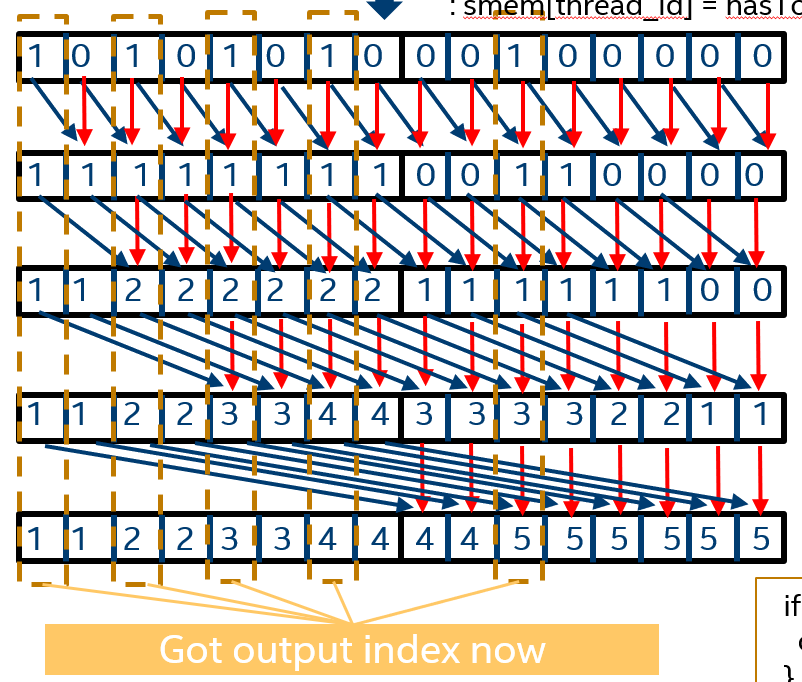
1 | if (hasTopk) { |
Sort for the top k value
Bitonic sorter
Bitonic sort is a sorting algorithm designed specially for parallel machines.
sequence is called Bitonic if it is first increasing, then decreasing. In other words, an array arr[0..n-i] is Bitonic if there exists an index i where 0<=i<=n-1 such that
**x0 <= x1 …..<= xi and xi >= xi+1….. >= xn-1 **
given a bitonic sequence, if we apply recursively these operations we get a sorted sequence.
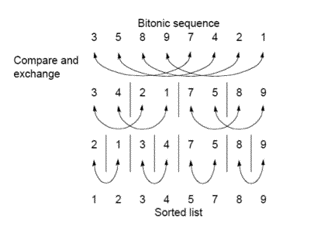
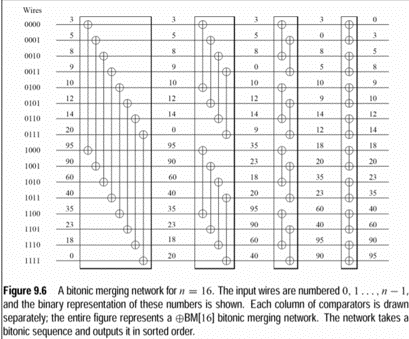
Bitonic sorter
Unsorted squence -> bitornic squence -> sorted sequence